|

闭环ABCD的4段线簇并不是都十分集中,往往出现偏离现象,有些还相当严重,这就充分表明熔滴短路过渡中出现了不规则现象,反应电弧燃烧过程的不稳定性。
比较两个图,当U=26V时的$% 线簇很分散,U=24V时的BC线簇相对集中。可见在U=26V的情况下,燃弧的短路电流上升的程度各不相同,分散性很大,短路过程不规则;另外,U=26V时的左上角与纵坐标接触,说明出现了电流为零的情况,即发生了断弧。还有,从图中可看出,U=24V时的****电流比U=26V时的****电流值低,引弧更容易,因此说明在电弧电压为24V时,熔滴过渡均匀,焊接过程稳定。
1.3 由电压及电流概率分布图分析电弧电压对电弧稳定性的影响
所谓电压概率密度分布,即把所测试的连续的电压区间分成间断的点,如电压0-40V内则可分为0、0.5、1.0、1.5…这样的电压,即区间间隔值ΔU=0.5V,然后统计这些电压值点的概率,即统计测试点中有多少属于同一电压值的点,接着把这些统计值描在N-U坐标系内,逐渐连线就成为电压概率分布[4]。电流概率密度分布与电压概率分布相似,只是其变化区间要大的多,为48-412A,其区间间隔ΔI=4.0A。
3组试验的电压和电流概率分布如图4所示,电压概率分布图的前一个波峰所处的电压较低,为短路过程;后一个波峰所处的电压较高,为燃弧过程,波峰的相对宽度能说明焊接过程中电弧是否稳定。由图可知,电弧电压较低的一组(U=24V时)最稳定,因为其不管是短路期间还是燃弧期间,电弧电压均围绕着两明显的峰值小范围分布,最高电压(再引弧电压)33.5V为3条曲线中的最小值,且其对应的电流概率分布中的峰值电流也最小。相反,当电弧电压为;24V和28V 时,其短路期间和燃弧期间的电压围绕峰值的分布范围均比电压为24V 时的要宽一些,说明无论是短路期间还是燃弧期间,电压的波动都更大,电弧的稳定性也就更差,同时最高电压比24V时高,表明它们在引弧时较之24V时更难。
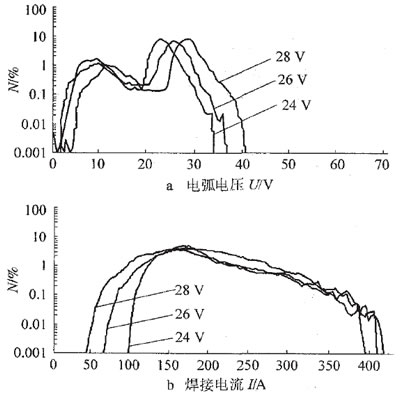
图4 混合气体焊电弧电压及焊接电流的概率密度分布图
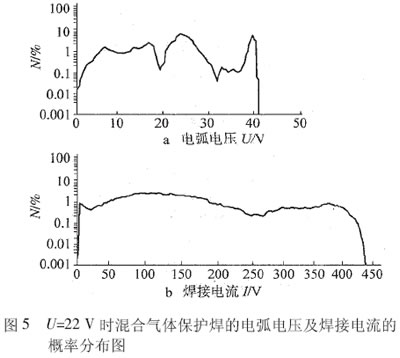
电弧电压为22V时的电弧电压和焊接电流概率密度分布如图5所示。电压概率分布出现了3个波峰,其中前两个波峰对应短路阶段,不仅短路的电压变化大(从0-30),而且其概率都比较小;后一个波峰对应燃弧阶段,虽说其围绕峰值小范围分布,但同时也说明其燃弧时间短,充分体现了熔滴过渡的不规则性。再看电流概率分布,其最高电流(峰值电流)不仅高,引弧困难,而且出现了电流为0的情况,即发生了断弧现象,表明了弧焊过程的不稳定性。
1.4 由短路时间频数分布图分析电弧电压对电弧稳定性的影响
短路时间频数分布是先统计测试过程中短路的总次数,然后以100μs 为区间间隔值,从0开始,把一次短路时间分别为0、100 μs,200μs…的次数统计出来,分别计算出其概率,即统计测试点中有多少属于同一短路时间值,接着把这些统计值描在N-T 坐标系内,组成短路时间频数直方分布图[5],从而对电弧燃烧的稳定性做出一定的分析。理想的短路时间频数分布应为中间高而两边低。
电弧电压为28V、26V的短路时间频数分布如图6所示。从图6a中可以看出,在短路时间为0.3ms时出现概率****值(超过10%),短路时间过短,说明出现了大量的瞬时短路,即焊接过程中刚短路时,电流刚开始上升,电弧又被重新点燃。在这种情况下,熔滴并没发生正常过渡,只是与熔池刚开始接触就可能发生了飞溅,影响焊接质量;另外在短路时间为2.2ms时也出现概率较大值(同样也超过了10%),短路时间过长,说明出现了熔滴与熔池长时间接触,而不能正常过渡,其随着输入热量的增加,有可能引起过渡过程中发生严重的飞溅,甚至引起焊丝的成段爆断,严重影响焊接过程和焊接生产率。 |
